Whenever I sign up for a new service– online or otherwise– and they want an email address, I create a custom address that identifies the company. For example, when I signed up for Vonage a few years ago, I used jeff-vonage@neobox.net. The reason? If I start getting spam at that address, I know exactly who sold my information (or whose customer database was compromised).
Behold one of many spam messages I received today:
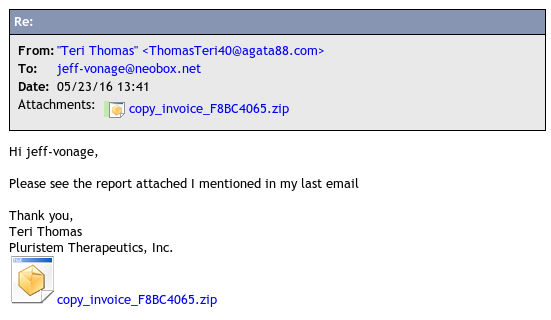
Yep, there’s the Vonage spam-trap address. Since it’s highly unlikely a spammer would guess that, it’s clear that Vonage either sold my information or lost their customer data. Either way, shame on you, Vonage.
As an aside, if I’m signing up for a new service where I don’t care whether they ever email me, I use guy@place.com. To whoever owns the place.com domain– especially if your name is Guy– I’m really sorry.